Geostandards Newsletter 20, 217–245 (1996)
A Self-Consistent Compilation
of Elemental Concentration Data
for 93 Geochemical Reference Samples
Department of Earth and Planetary Sciences and
McDonnell Center for the Space Sciences,
Washington University, St. Louis, MO 63130
U. S. A.
Concentration data obtained by instrumental neutron activation analysis are presented for up to 36 chemical elements in 93 geochemical reference samples, including some for which there are little previous data. Because all data are based on at least three independent analyses, and for many of the data the uncertainty associated with counting is an insignificant source of error, the values presented here are of higher precision than generally reported by INAA. Information on subsampling error (sample heterogeneity) is also presented.
INTRODUCTION
This paper presents elemental concentration data obtained by INAA (instrumental thermal neutron activation analysis) for 93 international geostandards (geochemical reference samples). We have obtained these data over a period of eleven years during which time we have analyzed approximately 11,700 terrestrial, lunar, and meteoritic samples for a variety of research projects. (Throughout this work, I use "we" to mean "I and other personnel of this laboratory;" see acknowledgments.) The geostandards were analyzed as quality control standards with each batch of research samples and several of the geostandards (Table 1) are ones for which there are few published data. Because each analyzed subsample of geostandard was irradiated with a large thermal neutron fluence (>2´ 1018 cm–2, time integrated flux) and radioassayed on several occasions for long durations and because all averages are based on analyses of at least three (usually, four or more) subsamples, the data presented here are more precise than those typically reported by INAA.
ANALYTICAL PROCEDURES, SUBSAMPLING, AND STANDARDS
During the eleven years these data were collected, we have constantly improved laboratory equipment and procedures. Nearly all of the data reported here, however, were obtained by the following procedures.
Most research done in this laboratory involves small, irreplaceable samples (e.g., 1,2), so procedures are optimized for small samples and the largest mass of powdered material that we can easily accommodate is about 250 mg. Thus in a typical analysis, 100–250 mg of each geostandard (hereafter, a "subsample") was sealed in a tube of ultrapure fused silica and irradiated for 12 hours in a thermal neutron flux of approximately 5´ 1013 cm-2s-1. Each tube received at least two radioassays of 2–12 hours duration between 7 and 13 days following irradiation; the two radioassays were each done using different detectors. This procedure was repeated between 28 and 35 days following irradiation. For most analyses, the tubes also received two 10–20 minute radioassays between 6 and 7 days following irradiation. Thus a single analysis is based on 4–6 separate radioassays of a subsample and the corresponding standards. Because for typical geologic materials in the 100–250-mg mass range we have repeatedly determined that tube blanks are negligible, each subsample was radioassayed in the tube in which it was irradiated, except for SARM 43 and SARM 49 (below), which have very low concentrations of most elements.
Except for SRM 1633a and 1633b, which we ground prior to use (3), we took all materials (geostandards treated as unknowns and comparator standards) directly from the containers in which they were stored and sealed them into irradiation tubes without pulverizing or drying them in order to minimize the possibility of contamination. Thus, all data presented here are on a "wet-weight" basis (i.e., micrograms of element per gram of undried sample). Data for LOD (loss on drying) at 110° C are presented in the tables and may be used for correction to dry-weight basis; LOD data are based on one or two determinations each. Also listed are the total number of analyses, n, and the total mass of analyzed material, mt. The value mt /n gives the average subsample mass per analysis, usually 100–250 mg. For a given geostandard, however, the actual subsample mass may have varied by more than a factor of two from analysis to analysis depending on the average mass of the research samples analyzed concurrently. Smaller average subsample masses were used for geostandards that contain high concentrations of elements that activate strongly (e.g., DTS-1 and MA-N) than for those that contain low concentrations (e.g., SARM 49).
I obtained all data reported here by comparison to multielement working standards of known composition. I obtained all "known compositions" for the working standards by standardization against either chemical standards or other working standards which in turn had been standardized directly against chemical standards (4). For Na, Ca, and W, AN-G (Greenland anorthosite, GIT-IWG) was the working standard, and for most other elements, SRM 1633a (coal flyash, NIST standard reference material) was the working standard (concentration values from reference [4], except that for Tb, a concentration of 2.53 µg/g was used as a result of restandardization in 1988). For many analyses, concentrations for some elements were determined against other working standards (including in-house synthetic standards) which I have standardized against SRM 1633a (Rb, Sr), primary chemical standards (Zn, Zr, Au, Ir), or DTS-1 (Cr, Ni; values from reference [4]). Thus none of the data presented here are based on "recommended" or "consensus" values from the literature. Some elements were not determined in every analysis because an appropriate standard was not included with every batch. In particular, K, Zn, Au, and Ir results are usually based on fewer analyses than the value of n (number of analyses) listed in the tables. Also, we do not report concentrations for Zn in geostandards for which the Zn/Sc concentration ratio is less than 50. With lower ratios, the values we obtain for Zn are systematically high and not reliably correctable because of the spectral interference from the large 1120.5 keV peak of 46Sc on the 1115.5 keV peak of 65Zn. Only for SARM 46, SARM 51, and SARM 52 (contaminated soils) were Cd and Hg concentrations determined.
Typically, we irradiated and radioassayed samples in batches of approximately 60 tubes, which consisted of two tubes of SRM 1633a, one or two tubes of AN-G, one tube each of one or two secondary working standards, approximately 50 tubes of research samples, and four to six tubes of geostandards (treated as "unknowns") with compositions similar to the research samples. However, in order to minimize certain possible sources of systematic error in the averages calculated for any given geostandard (e.g., flux heterogeneity, below), only one subsample of any given geostandard was analyzed in each batch.
Photopeak integrations and data reduction were done with the TEABAGS programs of Lindstrom and Korotev (5), which have undergone constant refinement during the period, including a major upgrade in 1987 for implementation on a microVAX® II (Digital Equipment Corporation). These programs include corrections for interferences from products of 235U fission (6). Some other general experimental details are described in Korotev (7).
RESULTS
Average concentrations obtained for the geostandards are presented in Table A1. The estimated precision of each value is indicated according to the key of Table 2. If for the most sensitive photopeak of an element, A is the integrated number of counts above background and s is the standard deviation based on counting statistics associated with A in a given analysis, and if s routinely exceeded A in different analyses of a given geostandard, then a detection limit is given instead of a concentration value. This detection limit or "less than" (<) value corresponds to the concentration value calculated from 3s (instead of A) for a typical analysis. "Not analyzed" usually indicates that the three analyses required to calculate a mean were not obtained because an appropriate standard was not included for the element in every analysis (e.g., Au). It is also used to indicate that interferences consistently prevented a reliable concentration or upper-limit value from being obtained (e.g., Zn). For some geostandards for which we have several analyses, the distribution of concentration values leads us to suspect that the element was not uniformly distributed among the analyzed subsamples. The corresponding mean value (Table A1) is flagged with an "H" or "h" superscript, according to the key of Table 2. I have also provided estimates of the concentrations of those rare earth elements (REEs) which were not analyzed directly. Each of these issues is discussed in more detail in the following sections.
Precision
As a result of the high neutron fluence, redundant radioassays, and long radioassay times, elemental concentration values reported here are based on large numbers of counts. For example, in a typical analysis of BCR-1, the total number of net photopeak counts upon which a concentration value is based exceeded 107 for Sc and Fe, 106 for Na, La, and Sm, and 105 for Eu and Lu. Even for Rb, an insensitive element at low concentration (49 µg/g) in BCR-1, a total of 7´104 counts was typically obtained. Thus for many data presented here, "counting statistics" are not the principal source of uncertainty. Other major sources of random uncertainty are (1) inhomogeneity of the neutron flux, (2) variation in water concentration (LOD) associated with using undried powders in conditions of variable relative humidity, and (3) actual differences in composition among analyzed subsamples (see "Subsampling error," below). Sample-to-detector geometry effects are not a substantial source of random error because we match subsample volumes in a given experiment and rotate tubes during radioassay using detectors with horizontal cryostats (7).
All concentration data presented here are means of three or more (![]() ) independent analyses, i.e., different
subsamples of a geostandard analyzed in different batches against different
subsamples of comparator standards. For elements such as Na, Sc, and
Sm for which concentrations in any given analysis are based on more than
106 total counts, the ratio of the sample standard deviation, s,
to the mean concentration of the n analyses,
) independent analyses, i.e., different
subsamples of a geostandard analyzed in different batches against different
subsamples of comparator standards. For elements such as Na, Sc, and
Sm for which concentrations in any given analysis are based on more than
106 total counts, the ratio of the sample standard deviation, s,
to the mean concentration of the n analyses, ![]() , is typically 0.007–0.013 for
any geostandard for which we have many analyses (e.g., n > 8),
if the geostandard is uniform in composition. If counting statistics
were the only source of error, we would expect
, is typically 0.007–0.013 for
any geostandard for which we have many analyses (e.g., n > 8),
if the geostandard is uniform in composition. If counting statistics
were the only source of error, we would expect ![]() to
be 0.001 (=
to
be 0.001 (=![]() ) or less. Thus ~1% RSD (relative standard
deviation,
) or less. Thus ~1% RSD (relative standard
deviation, ![]() ) is effectively
the lower limit of our batch-to-batch precision.
) is effectively
the lower limit of our batch-to-batch precision.
I believe that the largest source of this uncertainty, i.e., the largest source of error in a single analysis for elements for which counting statistics are a negligible source of uncertainty, is "flux heterogeneity," specifically, a slight difference in thermal neutron flux between a tube containing an "unknown" (subsample of a geostandard) and one containing a comparator standard (known composition). As a consequence, intrabatch precision is usually better than interbatch precision because within a batch, all samples are compared against the same tube of comparator standard for any given element. Another consequence of flux heterogeneity is that an analysis of a particular subsample that yields a concentration for Fe that is 0.5% lower, for example, than the mean concentration obtained in many analyses is likely to also yield concentrations of Sc, La, and Hf that are 0.5% low compared to their respective means. This occurs because in any given analysis, all of these elements are determined against the same tube of comparator standard (SRM 1633a), which may have a received a higher neutron flux than the tube containing the subsample of interest. However, in a subsequent analysis of the same geostandard, there is as equal probability that flux heterogeneity will lead to results that are 0.5% high. Thus I have minimized the effect of this source of systematic error by taking the mean of results obtained in several analyses (i.e., different irradiations) because over several analyses there is no mechanism that would lead to a particular geostandard (e.g., BHVO-1) consistently receiving a systematically low or high flux with respect to the comparator standards. [The possible exception, of course, is that a geostandard containing a particularly high concentration of B, Cd, or some other strong absorber of thermal neutrons could receive a consistently low average dose, but calculations verify that it is unlikely that the "thin" target approximation (e.g., 8) is violated for any of the geostandards analyzed here.]
I have calculated "best values" as follows. For each concentration
value x obtained from a single analysis there is an associated
estimate, ![]() , of the standard deviation of the population of all such
values (n = ¥), where
, of the standard deviation of the population of all such
values (n = ¥), where
![]() ,
Eqn. 1
,
Eqn. 1
![]() is the standard deviation
associated with counting statistics, and
is the standard deviation
associated with counting statistics, and ![]() is
an estimate of the interbatch standard deviation, which I assume to be
equal to 1% of the concentration value
is
an estimate of the interbatch standard deviation, which I assume to be
equal to 1% of the concentration value ![]() .
As noted above, for elements and samples for which
.
As noted above, for elements and samples for which ![]() is
negligible compared to
is
negligible compared to ![]() ,
, ![]() is essentially identical for all analyses,
i.e.,
is essentially identical for all analyses,
i.e., ![]() is ~1% of the concentration
value. In this case, I calculate the best value,
is ~1% of the concentration
value. In this case, I calculate the best value, ![]() ,
as the simple mean,
,
as the simple mean, ![]() , of
all n analyses
, of
all n analyses
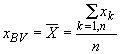 Eqn. 2 (
Eqn. 2 (![]() )
)
and I calculate a 95% confidence limit, ![]() ,
from the sample standard deviation, s, and Student’s t factor
in the usual manner,
,
from the sample standard deviation, s, and Student’s t factor
in the usual manner,
![]() Eqn. 3
Eqn. 3
(e.g., 9).
For elements and samples for which ![]() is negligible compared to
is negligible compared to ![]() ,
i.e., when counting precision dominates
,
i.e., when counting precision dominates ![]() , values of
, values of ![]() are
usually variable from analysis to analysis depending on a variety of
analytical factors that vary from batch to batch, most notably sample
mass, radioassay time, sample-to-detector distance, and decay time. For
example, a Zr concentration obtained from one analysis might be 200 ± 20 µg/g
(i.e.,
are
usually variable from analysis to analysis depending on a variety of
analytical factors that vary from batch to batch, most notably sample
mass, radioassay time, sample-to-detector distance, and decay time. For
example, a Zr concentration obtained from one analysis might be 200 ± 20 µg/g
(i.e., ![]() ) while that from
a second analysis might be 193 ± 7 µg/g (i.e.,
) while that from
a second analysis might be 193 ± 7 µg/g (i.e., ![]() ). In this case, I calculate the best value as the se-weighted
mean,
). In this case, I calculate the best value as the se-weighted
mean, ![]() , where
, where
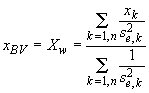 Eqn. 4 (
Eqn. 4 (![]() )
)
and I calculate the 95% confidence limit ![]() as
as
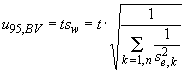 Eqn. 5
Eqn. 5
Operationally, if ![]() averages
less than 3%, I have calculated the best value
averages
less than 3%, I have calculated the best value ![]() as
the simple mean
as
the simple mean ![]() , otherwise
the best value is the uncertainty-weighted mean
, otherwise
the best value is the uncertainty-weighted mean ![]() .
[Certain exceptions to this general rule are discussed in the next section.]
In Table A1, best values are coded by precision according
to the relative 95% confidence limit,
.
[Certain exceptions to this general rule are discussed in the next section.]
In Table A1, best values are coded by precision according
to the relative 95% confidence limit, ![]() , and the key of Table 2. For example, for bold-faced values,
, and the key of Table 2. For example, for bold-faced values, ![]() <3%.
<3%.
Subsampling error
One important cause of imprecision in geostandards data is actual variation in the concentration of an element among different analyzed subsamples. I shall refer to this reality of rock analysis as subsampling error. Subsampling error is often designated "sample heterogeneity," a misleading term because, as noted by Ingamells and Switzer (10), no mixture of minerals can be truly homogeneous, regardless of how finely pulverized or well mixed.
To evaluate subsampling error, I have used the following procedure.
For each element in each sample, I have compared (one-sided F test
at 95% confidence) the total variance, s2, associated
with ![]() (Eqn. 2) to the estimated variance associated with analytical uncertainty,
(Eqn. 2) to the estimated variance associated with analytical uncertainty, ![]() , where
, where ![]() is the average of
is the average of ![]() (Eqn.
1) for all subsamples. In some cases s2 significantly
exceeds
(Eqn.
1) for all subsamples. In some cases s2 significantly
exceeds ![]() , from which I infer that a portion
of the observed scatter results from subsampling error. Instances of
subsampling error revealed by this procedure are indicated in Table A1 by an "H" or "h" superscript,
but only when
, from which I infer that a portion
of the observed scatter results from subsampling error. Instances of
subsampling error revealed by this procedure are indicated in Table A1 by an "H" or "h" superscript,
but only when ![]() exceeds 5% (Table 2). If I have underestimated the analytical uncertainty,
exceeds 5% (Table 2). If I have underestimated the analytical uncertainty, ![]() , the procedure will erroneously ascribe some unrecognized source
of analytical uncertainty to subsampling error. However, most of the
instances of subsampling error indicated in Table A1 are geochemically reasonable, thus I assume
the procedure is generally valid. I discuss some systematic occurrences
of subsampling error below.
, the procedure will erroneously ascribe some unrecognized source
of analytical uncertainty to subsampling error. However, most of the
instances of subsampling error indicated in Table A1 are geochemically reasonable, thus I assume
the procedure is generally valid. I discuss some systematic occurrences
of subsampling error below.
As expected, subsampling error occurs frequently for elements such as Cr, Zr, Hf, Th, U that are carried primarily by trace minerals in which the elements occur in high concentration (chromite, zircon). Similarly, in most geostandards for which we detect Au, subsampling error is serious for Au because most of the Au occurs in metallic form. Also as expected, some of the worst instances of subsampling error occur in coarse-grained, evolved rock types. For example, for all three of the GSJ granodiorite and granite samples, subsampling error is serious, particularly for the REE (rare earth elements; Fig. 1). These geostandards are not finely pulverized and grains of different colors are easily visible in the samples to the naked eye. Among subsamples, concentrations of LREE (light REE, La and Ce) tend to correlate with each other and those of HREE (heavy REE, Yb and Lu) also correlate, but the LREE do not usually correlate with the HREE. This indicates that at least two REE-rich minerals are involved. I have observed similar, but less severe, behavior in granodiorite GSP-1 (3). For several monomineralic geostandards with very low concentrations of most elements (feldspars, quartz), subsampling error is a major cause of subsample to subsample variation in concentrations for REE, Hf, Ta, Th, and U.
In many geostandards, As and Sb are nonuniformly distributed. Some of the worst subsampling errors that we observe involve Sb. Some subsamples of some geostandards have anomalously high concentrations of Sb; this is particularly evident in AN-G and SRM 278 because we have analyzed these materials many times (Fig. 2). Curiously, AN-G (anorthosite) is one of the few geostandards that, during its preparation (11), was ground in tungsten carbide, which is highly efficient at pulverizing and mixing samples. Similarly, subsampling error is usually not observed in glassy samples like SRM 278 (obsidian). We do not observe subsampling error for any other elements (except Au) in either AN-G or SRM 278. Together these observations suggest that the high Sb concentrations we occasionally observe in these two geostandards (and possibly those we observe in others, as well) are somehow associated with post-grinding contamination or possibly sporadic blank problems during analysis (e.g., Sb contaminated silica tubes). However, other samples that we have analyzed many times during the same time period do not show Sb anomalies (Fig. 2), so I discount blanks as the source of the problem. We obtain Sb concentrations via both short-lived 122Sb and the long-lived 124Sb (4); the values routinely agree within counting statistics. Thus I conclude that the Sb anomalies are a property of some geostandards and not related to our analytical procedure.
In a few cases where subsampling error is serious and n is sufficiently large that it is evident that the distribution of values is not normal (as in AN-G; Fig. 2), I report mass-weighted means as best values because these should best represent the concentration in a large subsample. I emphasize that subsampling errors reported here are aggravated by the relatively small sample masses used (0.1–0.25 g) and that the magnitude of the error in many cases is small and only apparent because of the high precision.
DISCUSSION
Accuracy
I have made two tests of accuracy of the best values presented here.
First, I have compared differences between our BVs (best values, ![]() ) and RVs (recommended, consensus, or working values,
) and RVs (recommended, consensus, or working values, ![]() ). Second, I have compared ratios of
our BVs to the RVs. A difficulty in making such comparisons is that some
RVs are known to a high degree of precision (e.g., <1%) while others
are known only poorly. Similarly, although our data for some elements
are precise, our data for other elements are routinely of poor precision
compared to data upon which RVs are based because INAA is not the most
precise technique for those elements (e.g., Sr and Nd). Thus comparisons
are based only on data for geostandards for which 95% confidence limits, u95,RV,
are explicitly stated (12) or can be calculated (e.g., Eqn. 3) from the
data presented (13, 14). Although I do not regard these as ultimate tests,
they provide a focus for discussion.
). Second, I have compared ratios of
our BVs to the RVs. A difficulty in making such comparisons is that some
RVs are known to a high degree of precision (e.g., <1%) while others
are known only poorly. Similarly, although our data for some elements
are precise, our data for other elements are routinely of poor precision
compared to data upon which RVs are based because INAA is not the most
precise technique for those elements (e.g., Sr and Nd). Thus comparisons
are based only on data for geostandards for which 95% confidence limits, u95,RV,
are explicitly stated (12) or can be calculated (e.g., Eqn. 3) from the
data presented (13, 14). Although I do not regard these as ultimate tests,
they provide a focus for discussion.
Differences
For the difference test I compare 671 pairs of values in 29 geostandards,
ranging from 13 elements in PCC-1 to 31 elements in SCo-1. (For this
test, rare earth elements for which concentrations were estimated were
not included; see below.) I define the maximum uncertainty, ![]() ,
as the greater of u95,BV or u95,RV and
ignore the smaller uncertainty. The absolute test of agreement is whether
,
as the greater of u95,BV or u95,RV and
ignore the smaller uncertainty. The absolute test of agreement is whether ![]() .
However, this simple test often suggests disagreement for values that
differ by only a few percent when the relative value of
.
However, this simple test often suggests disagreement for values that
differ by only a few percent when the relative value of ![]() is
very low, as for Fe in most geostandards, because both the RVs and BVs
are very precise. Thus for the difference test, I include a "relative
difference" criterion in addition to the "absolute difference" criterion.
The result of the difference test is that 628 of the tested BVs agree
with the RVs in that
is
very low, as for Fe in most geostandards, because both the RVs and BVs
are very precise. Thus for the difference test, I include a "relative
difference" criterion in addition to the "absolute difference" criterion.
The result of the difference test is that 628 of the tested BVs agree
with the RVs in that ![]() or
or ![]() , that is, 93.6%
of our best values agree within 10% of the RV or within the maximum uncertainty.
The success rate is reduced to 79% for a 3% relative difference criterion
and 75% for a 1% criterion. I believe that in several of the instances
in which our BV differs by more than 10% from the RV, as well as some
other cases of lesser disagreement, that the RV is inaccurate. I discuss
three types of systematic disagreement below.
, that is, 93.6%
of our best values agree within 10% of the RV or within the maximum uncertainty.
The success rate is reduced to 79% for a 3% relative difference criterion
and 75% for a 1% criterion. I believe that in several of the instances
in which our BV differs by more than 10% from the RV, as well as some
other cases of lesser disagreement, that the RV is inaccurate. I discuss
three types of systematic disagreement below.
Several instances of severe disagreement involve Cr at low concentration. For example, we obtain 10.8 ± 0.3, 8.7 ± 0.2, and 2.80 ± 0.13 µg/g Cr in BCR-1, AGV-1, and RGM-1, compared to RVs of 16, 10.1, and 3.7 µg/g. Comparison for the other geostandards show that our agreement is good for Cr at high concentration (Table 3), but that our values are sometimes low compared to RVs at low concentrations of Cr. The cause of our low values, particularly compared to other INAA data, is that I make interference corrections on the 320.1 keV peak of 51Cr from 177Lu at 321.3 keV and 147Nd at 319.4 keV when these interfering peaks are unresolved from the peak of interest, which is usually the case. These two interferences are so severe that in silicic rocks like AC-E we can see no signal for 51Cr in the presence of the peaks for the two interfering isotopes; as a result, I report <2 µg/g for Cr in AC-E. If we do not make these corrections, concentrations we obtain for Cr in low-Cr samples are more nearly consistent with the RVs. I suspect, however, that some recommended values for Cr in low-Cr rocks are erroneously high because of inclusion in the averages of INAA data for which these corrections were not made.
Similarly, another systematic discrepancy involves Na at low concentration. In Mg-rich, ultramafic samples such as PCC-1, DTS-1, and UB-N, a significant fraction of the 24Na derives from Mg via the 24Mg (n,p) 24Na reaction. We make a correction of 1.6´ 10–4 apparent percent Na per percent Mg (updated from reference 4), which is approximately a –50% correction for high-Mg/Na samples like DTS-1 and PCC-1. In ultramafic rocks, Na concentrations are near the detection limits of several other techniques, although not INAA. Thus recommended values for Na are dominated by INAA data, some of which I suspect are erroneously high from failure to correct for the nuclear interference from Mg.
A third source of systematic discrepancy between our values and some published RVs involves corrections we apply to Zr, Ba, La, Ce, Nd, and Sm for nuclear or spectral interferences associated with fission of 235U in the sample (6). Though we apply the corrections to all samples regardless of U concentration, they are particularly important for high-U samples like SARM 48 and GXR-1. For pegmatitic granite MA-N, the problem is so critical that virtually the entire signal for 140La, 141Ce, and 147Nd is from the (n,fission) reaction on 235U, not the (n,g) reaction on REE isotopes (15).
Ratios
In order to reveal possible systematic errors, I have evaluated our
BVs for 29 well-characterized geostandards by simply computing the ratio ![]() for each element in each geostandard and calculating for
each element the mean ratio and 95% confidence limit on that mean. If
the mean ratio is significantly different from unity, then a systematic
error is indicated. For this comparison I ignore uncertainties on the
BVs and RVs, except that I have excluded from the comparison any BV-RV
pair for which the confidence limits are greater than 10% of the value
(i.e.,
for each element in each geostandard and calculating for
each element the mean ratio and 95% confidence limit on that mean. If
the mean ratio is significantly different from unity, then a systematic
error is indicated. For this comparison I ignore uncertainties on the
BVs and RVs, except that I have excluded from the comparison any BV-RV
pair for which the confidence limits are greater than 10% of the value
(i.e., ![]() or
or ![]() ); thus n < 29 for all elements.
); thus n < 29 for all elements.
The results show that for many elements our BVs are systematically low or high compared to the recommended values, but that the relative errors are small, <5% for all elements except Ta (Table 3). For example, our BVs are significantly (95% confidence) and systematically high for Sr, on average, but only by a factor of 1.014. The most serious disagreement is that our BVs for Ta are low by 6.7%, on average, compared to the RVs. I do not know the cause of discrepancies such as this, but cannot discount systematic errors in the concentration values of our working standards.
Some problems associated with using working values
The recent compilation of "working values with confidence limits for twenty-six CRPG, ANRT, and IWG-GIT geostandards" (12) is extremely useful for making comparisons such as those discussed above as data for 16 of the 29 geostandards evaluated were taken from that source. In making the comparisons I discovered a number of disagreements between our best values and the recommended or working values that were the result of problems with working values or the corresponding confidence limits. I discuss those problems here for consideration by future compilers of data.
Three classes of problem were encountered. First, in a few cases there are obvious errors in working values, i.e., the working value is clearly inconsistent with the available data (e.g., Zn in GH, Y in DT-N, and Cs in UB-N; 16,17). There are other instances where working values fall in the range of reported data, but do not appear to correspond to means or modes, even after exclusion of aberrant data that might justifiably be excluded (e.g., La and Eu in GS-N; 17). Second, in some cases our values fail to "agree" with working values only because the working values are not stated to a number of significant digits justified by the confidence limit. For Sm in UB-N, for example, I obtain a best value of 0.214 ± 0.003 µg/g. By the difference test described above, this value fails to agree with the working value, "0.2 ± 0.01." However, the actual mean and 95% confidence limit calculated from the 7 data upon which the working value is based is 0.206 ± 0.009 (17) and our best value does, in fact, fall within this range. The advantage or rationale of expressing working values to fewer decimal places than that of the stated confidence limits is not evident to this geochemist (e.g., Sr in UB-N: 9 ± 1.85; 12). Third, there are a number of instances where the stated confidence limit is smaller by a factor of at least two than is justified by the data upon which the working value is apparently based (e.g., Sb and Hf in BR, Hf in DT-N, Ta in Mica-Fe; 16,17). For the purpose of the comparisons discussed in this section, I have either modified a few (<12) working values and confidence limits to be consistent with available data or not included the data in the comparison where the source of the problem was not clear (e.g., La and Eu in GS-N).
Rare earth elements
Data quality for the REEs can be judged by the smoothness of the REE "pattern," i.e., a plot of normalized concentrations against atomic number or inverse ionic radius (e.g., 18, 19). The REEs are unique in that, because of their geochemical coherence, "bad" values for one REE can sometimes be detected based on concentrations of other REEs. The benefits of this characteristic are generally not utilized in generating recommended values for the REEs in geostandards and, in fact, in some compilations RVs are not stated to enough digits to generate smooth REE patterns.
This laboratory has a long-standing interest in the geochemistry of the REEs (e.g., 18, 20–22) and I have expended more effort in obtaining accurate data for the REEs than some other elements. An apparent disadvantage of INAA compared to some other techniques is that only some of the REEs can be determined. Under our operating conditions, we routinely obtain precise data for 7 of the 14 naturally occurring REEs, with an eighth, Nd, determined less precisely. However through the benevolence of nuclear fate, some light, middle, and heavy REEs can be determined by INAA, as well as anomalously behaving Eu and Ce. Thus the eight elements that we determine are sufficient in nearly all circumstances we have encountered to characterize adequately the "REE pattern" of a rock or mineral. For all but a few geochemical problems, having additional data for the missing elements would not influence the geochemical interpretation.
For reference, I have included plots of chondrite-normalized REE concentrations for each of the geostandards analyzed here as Fig. A1 (except for a few, in which REE concentrations are below detection limits, e.g., DTS-1 and MA-N). By interpolation (and, for Gd, some subjective extrapolation), the preparation of REE plots based on precise data for measured REEs allows us to make accurate estimates of the concentrations of REEs not measured directly (18). In fact, using this procedure I can estimate the concentration of Nd in most rocks more accurately than I can determine it through direct analysis. Thus for reference, I include for most of the analyzed geostandards estimates of concentrations of REEs not measured directly, including Y [in square brackets]. This procedure cannot be used for samples where REE concentrations are affected by industrial contamination (SARM 46 and SARM 52). Also, it may not reliably estimate Pr in samples where Ce behaves anomalously and there is "curvature" to the REE pattern (e.g., SRM 69b). The estimate for Y assumes that the element plots halfway between Ho and Er on the plots of Fig. A1.
Although it is not customary to report estimated concentrations in compilations such as this, the data of Table 3 show that the estimates are usually accurate within 5% and are seldom in error by more than 10%, except perhaps for Gd, thus these estimates should be useful for some applications.
Special features
In this section I discuss special features of some of the geostandards.
USGS
I include data for four geostandards that have been described but have had only limited distribution: ATT-1, CSB-1, GSM-1, and TLM-1 (23, 24).
NIST
Subsampling error is serious for SRM 70a (K feldspar) and 99a (Na feldspar) where concentrations of Cr, trivalent REE, Hf, Ta, Th, and U vary considerably among subsamples. Both SRM 278 (obsidian) and SRM 688 (basalt) have concentrations of Au that are anomalously high for the types of rocks they represent; the Au is not uniformly distributed among small subsamples and is almost certainly a contaminant. As discussed above, some subsamples of SRM 278 have anomalously high concentrations of Sb (Fig. 2).
CRPG, ANRT, and GIT-IWG
For granite GA, and to a lesser extent granite GH, there is a small
problem with variation in concentrations of incompatible trace elements
(REE, Hf, Ta, Th, U) from subsample to subsample. Total variance ![]() significantly
exceeds analytical variance
significantly
exceeds analytical variance ![]() for
both light and heavy trivalent REE in GA and the light REE in GH, but
the relative standard deviations are only about 3%, insufficient to trigger
the "h" flag (5%) of Table A1.
for
both light and heavy trivalent REE in GA and the light REE in GH, but
the relative standard deviations are only about 3%, insufficient to trigger
the "h" flag (5%) of Table A1.
For the two CRPG mica standards, we have analyzed both the powdered (p) and granular (g) allocations; the granular samples consist of unground mica grains. For Mica-Fe (biotite) we obtain virtually identical average concentrations for all elements except W (from tungsten carbide) in the two types of samples. Concentrations of REE, Th, and U are not uniform among subsamples of the granular sample, however. For Mica-Mg (muscovite), concentrations of most elements in the two sample types are also almost identical. However, concentrations of Sb, REE, W, Au, and Th are greater in the powdered allocation. Concentrations of all REE except Eu are below detection limits in the granular sample. In the powdered sample, REE concentrations are detectable, but light REE (La and Ce) are variable from subsample to subsample.
Despite having been ground in tungsten carbide, concentrations of several elements vary among subsamples of FK-N (K feldspar). We have only analyzed four subsamples of GL-O (glauconite), but for one of the subsamples, REE concentrations are about 12% lower and Th about 6% lower than the mean of the other three.
GSJ
As noted above, subsampling error is a problem for the granitoid samples (JG-1a, JG-2, and JG-3; Fig. 1) and, to a lesser extent, the feldspar samples (JF-1 and JF-2).
SABS
For most elements determined by INAA, SARM 49 (high purity quartz) and SARM 43 (magnesite) are at the low end of the range of concentrations among geostandards analyzed here. For some elements, our values are considerably less than the certified values (25), a circumstance I suspect is related to contamination and blank problems in some data upon which the certified values are based. In order to eliminate the potential for tube blanks causing systematic errors for any element in our analyses, for these two geostandards only I transferred the irradiated powders to unirradiated silica vials for radioassay. Subsampling error is serious for a number of elements in SARM 43 (As, Ba, LREE, Hf, Au, and Th) and is a lesser problem in SARM 49 (Cr, Fe, Co, LREE, Au, and Th).
The average mass of the eight analyzed subsamples of SARM 7 (Pt ore) was only 115 mg, compared to a recommended sample mass of >10 g when used as a precious-metal standard. As a result, subsampling error causes low precision for Ir and Au, as well as As, Sb, Hf, Ta, Th, and U. Despite the small subsamples, our average concentration (mass-weighted) for Ir is reasonable, 70 ng/g of Ir, compared with a certified value of 74 ± 12 ng/g. Our average Au concentration (mass-weighted), however, is low by a factor of two: 149 ng/g Au, compared to a certified value of 310 ± 15 ng/g. In one 50-mg subsample, we obtained concentrations of Co and W significantly greater than the mean of the other subsamples (Co: 128 µg/g, compared to 113 ± 1 µg/g; W: 187 µg/g, compared with <2 µg/g). I attribute these anomalies to a fragment of tungsten carbide and have excluded this subsample from the means for these two elements. No anomaly in Ta concentration was observed, which, like Co, is an additive in some commercial tungsten carbides.
The contaminated sediment samples, SARM 46, SARM 51, and SARM 52 each have "unnatural" REE patterns (Fig. A1.3) indicating contamination with REE, particularly Ce and Nd in SARM 46 and Ce in SARM 52. The REE are nonuniformly distributed in our small subsamples of SARM 46 (average mass: ~150 mg).
Acknowledgments. I thank Kaylynn Rockow, Brad Jolliff, and Alison Steele for their help in sample analysis, Larry Haskin for stimulating discussions and encouragement, and two unidentified reviewers for a number of useful comments and suggestions. This work was supported in part by the U. S. Department of Energy through grant DE-FG07-80ER10275 to the University of Missouri Research Reactor.
REFERENCES
(1) B. L. Jolliff, R. L. Korotev, and L. A. Haskin (1991)
A ferroan region of the lunar highlands as recorded in meteorites MAC88104
and MAC88105,
Geochim. Cosmochim. Acta 55: 3051–3071.
(2) Korotev R. L. (1994)
Compositional variation in Apollo 16 impact-melt breccias and inferences for
the geology and bombardment history of the Central Highlands of the Moon, Geochim.
Cosmochim. Acta 58: 3931–3969.
(3) R. L. Korotev (1987b)
Chemical homogeneity of National Bureau of Standards coal flyash (SRM 1633a), J. Radioanal.
Nucl. Chem., Art. 110: 179–189.
(4) R. L. Korotev (1987a)
National Bureau of Standards coal flyash (SRM 1633a) as a multielement standard
for instrumental neutron activation analysis, J. Radioanal. Nucl. Chem., Art. 110:
159–177.
(5) D. J. Lindstrom and R. L. Korotev (1982)
TEABAGS: Computer programs for instrumental neutron activation analysis, J.
Radioanal. Chem. 70: 439–458.
(6) R. L. Korotev and D. J. Lindstrom (1985)
Interferences from fission of 235U in INAA of rocks, Trans. Amer.
Nucl. Soc. 49: 177–178.
(7) R. L. Korotev (1991)
Geochemical stratigraphy of two regolith cores from the central highlands of
the Moon, Proc. Lunar Planet. Sci., Vol. 21, 229–289,
Lunar and Planetary Institute, Houston.
(8) L. A. Haskin and K. E. Ziege (1971)
Neutron activation: Techniques and possible uses in soil and plant analysis, Instrumental
Methods for Analysis of Soils and Plant Tissue, pp. 185–208, Soil
Science Society of America, Madison, Wisconsin.
(9) H. A. Laitinen (1960)
Chemical Analysis, McGraw-Hill, New York.
(10) C. O. Ingamells and P. Switzer (1973)
A proposed sampling constant for use in geochemical analysis, Talanta 20:
547–568.
(11) K. Govindaraju (1980)
Report (1980) on three GIT-IWG rock reference samples: Anorthosite from Greenland,
AN-G; Basalte d’Essey-la-Côte, BE-N; Granite de Beauvoir, MA-N, Geostandards
Newsletter 4: 49–138.
(12) K. Govindaraju (1995)
1995 working values with confidence limits for twenty-six CRPG, ANRT, and IWG-GIT
geostandards, Geostandards Newsletter 19: 1–32.
(13) E. S. Gladney and I. Roelandts (1988)
1987 compilation of elemental concentration data for USGS BHVO-1, MAG-1, QLO-1,
RGM-1, SCo-1, SDC-1, SGR-1, and STM-1, Geostandards Newsletter 12:
253–362.
(14) E. S. Gladney, E. A. Jones, E. J. Nickell, and I. Roelandts (1990)
1988 compilation of elemental concentration data for USGS basalt BCR-1, Geostandards
Newsletter 14: 209–359.
(15) K. Govindaraju and I. Roelandts (1993)
Second report (1993) on the first three GIT-IWG rock reference samples: Anorthosite
from Greenland, AN-G; Basalte d’Essey-la-Côte, BE-N; Granite de Beauvoir,
MA-N, Geostandards Newsletter 17: 227–294.
(16) K. Govindaraju and I. Roelandts (1988)
Compilation report (1966-1987) on trace elements in five CRPG geochemical reference
samples: basalt BR; granites, GA and GH; micas, biotite Mica-Fe and phlogopite
Mica-Mg, Geostandards Newsletter 12: 119–201.
(17) K. Govindaraju and I. Roelandts (1989)
1988 compilation report on trace elements in six ANRT rock reference samples:
diorite DR-N, serpentine UB-N, bauxite BX-N, disthene DT-N, granite GS-N
and potash feldspar FK-N, Geostandards Newsletter 13: 5–67.
(18) L. A. Haskin and R. L. Korotev (1973)
Determination of rare earths in geological and raw materials. In Analysis
and Application of Rare Earth Minerals, Odd B. Michaelson, ed., pp. 183–211,
NATO Advanced Study Institute, Universitetesforlaget, Oslo.
(19) U. Kramar and H. Puchelt (1982)
Reproducibility tests for INAA determinations with AGV-1, BCR-1 and GSP-1 and
new data for 17 geochemical reference materials, Geostandards Newsletter 16:
221–227.
(20) L. A. Haskin, T. R. Wildeman, and M. A. Haskin (1968)
An accurate procedure for the determination of the rare earths by neutron activation, J. Radioanal.
Chem. 1, 337–348.
(21) L. A. Haskin, P. A. Helmke, T. P. Paster, and R. O. Allen (1971)
Rare earths in meteoritic, terrestrial, and lunar matter. In Activation
Analysis in Geochemistry and Cosmochemistry, A. Brunfelt and E. Steinnes,
eds., Proceedings of the NATO Conference on Activation Analysis in Geochemistry,
p. 201–218, Universitetesforlaget, Oslo.
(22) L. P. Gromet, R. F. Dymek, L. A. Haskin, and R. L. Korotev (1984)
The "North American shale composite:" Its compilation, major and
trace element characteristics, Geochim. Cosmochim. Acta 48, 2469–2482.
(23) F. J. Flanagan (1986)
Rock reference samples, San Marcos gabbro, GSM-1, and Lakeview Mountain tonalite,
TLM-1, Geostandards Newsletter 10: 111–120.
(24) J. W. Hosterman and F. J. Flanagan (1987)
USGS reference samples attapulgite ATT-1 and bentonite CSB-1, Geostandards
Newsletter 11: 1–9.
(25) E. J. Ring (1993)
The preparation and certification of fourteen South African silicate rocks
for use as reference materials, Geostandards Newsletter 17:
137–158.
(26) E. S. Gladney, E. A. Jones, E. J. Nickell, and I. Roelandts (1991)
1988 compilation of elemental concentration data for USGS DTS-1, G-1, PCC-1,
and W-1, Geostandards Newsletter 15: 199–396.
(27) E. S. Gladney, E. A. Jones, E. J. Nickell, and I. Roelandts (1992)
1988 compilation of elemental concentration data for USGS AGV-1, GSP-1 and
G-2, Geostandards Newsletter 16: 111–300.
(28) K. Govindaraju (1987)
1987 compilation report on Ailsa Craig granite AC-E with participation of 128
GIT-IWG laboratories, Geostandards Newsletter 11: 203–255.
(29) K. Govindaraju, Potts P. J., Webb P. C., and Watson J. S. (1994)
1994 report on Whin sill dolerite WS-E from England and Pitscurrie microgabbro
PM-S from Scotland: Assessment by one hundred and four international laboratories, Geostandards
Newsletter 18: 211–300.
(30) N. Nakamura (1974)
Determination of REE, Ba, Fe, Mg, Na, and K in carbonaceous and ordinary chondrites, Geochim.
Cosmochim. Acta 38: 757–775.
(31) E. Anders and N. Grevesse (1989)
Abundances of the elements: Meteoritic and solar, Geochim. Cosmochim. Acta 53:
197–214.